Электрический сигнал

Типы электрических сигналов

В основу работы электронных схем положено прохождение электрических сигналов по электрическим цепям.
электрическая цепь - совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.
электрический сигнал – информация выраженная напряжением или током, проходящим по электрической цепи.

Основными характеристиками электрического сигнала является:

• Период — это отрезок времени, через который сигнал начинает повторяться. Это временное значение также называют временем периода для синусоид или шириной импульса для меандров и обозначают буквой T.
• Частота - это число раз, которое сигнал повторяет сам себя за период времени равный 1 секунде. Частота является величиной, обратной периоду времени, ( ). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду.
• Амплитуда — это величина изменения сигнала. Измеряется в Вольтах (В) или Амперах (А), в зависимости от того, какую временную зависимость (напряжения или тока) мы используем.

С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени. То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени.
Выделяют следующие типы сигналов:
Аналоговый сигнал – электрический сигнал непрерывный во времени, и максимально соответствующий по форме физическому сигналу который он передает (например: звук, температура и пр.). Такой способ передачи наиболее точно передает информацию о процессе, но имеет очень слабую помехозащищенность - малейшее отклонение в форме приводят к искажению. Защитить переносимый сигнал от искажений довольно проблематично.
Цифровой сигнал – комбинация коротких импульсов одинаковой амплитуды. Для представления информации физическая величина кодируются в числовые последовательности двоичного кода (амплитуда может принимать только два предельных значения - 0 и 1). Благодаря использованию возможности отклонений от уровней напряжения логических схем по амплитуде значительно повышена помехоустойчивость сигнала.

Возможность преобразования аналогового сигнала в цифровую форму (и обратно) определило широкое распространение цифровой техники. Высокая скорость работы аппаратуры позволяет в процессе преобразования получить сигнал высокой точности (с минимальными искажениями).

---

Уровни напряжения логических схем

Цифровые устройства оперируют с сигналами двух типов - "высокий логический уровень" (1) и "низкий логический уровень" (0). Полное напряжение питания принимается в качестве уровня "логической единицы", а нулевое напряжение - в качестве уровня "логического нуля".

В реальных схемах существует некоторое отклонение от идеала, например:
уровнями напряжения ТТЛ-схем (транзисторно-транзисторная логика) соответствуют напряжению около О В (земля) и напряжением от + 3 до + 5 В. При этом логическая единица находится в промежутке напряжений от 2,7 – 5 Вольт, логический нуль от 0 – 0,5 Вольт. Промежуток напряжений от 0,5 – 2,7 Вольт соответствует неопределенному состоянию, то есть никто не может предсказать к какому уровню перейдет сигнал.

Неопределенность уровня сигнала может происходить также в результате "дребезга контактов". Этот эффект происходит из-за вибрации механических переключателей, когда при единичном нажатии происходит выдача пачки импульсов, что не допустимо для большинства схем. Решением данной проблемы может быть введение емкости в цепь управления - RC-фильтр, а для микропроцессорных систем возможно программное создание временной задержки заведомо большей чем может происходить процесс.

Для понимания процессов при операциях с информацией в двоичной форме необходимы знания систем счисления, правила кодирования и навыки математических вычислений. Также предлагаем ознакомиться с разделом "Виды электрических сигналов"

---

двоичная математика:

Системы счисления

Система счисления

способ записи чисел с помощью заданного набора специальных знаков (цифр).

Символ

это знак, изображение какой-нибудь вещи или животного для обозначения качества предмета; условный знак каких-либо понятий, идей, явлений.

Число

основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы математических операций. Возникнув ещё в первобытном обществе из потребностей счёта.

Цифры

система знаков («буквы») для записи чисел («слов»).

Основание

количество цифр, используемых в системе счисления для записи чисел.

Существуют позиционные и непозиционные системы счисления.

Непозиционной системой счисления

называется система, в которой вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.

Позиционной системой счисления

называется система, в которой вес каждой цифры измеряется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.

Разряд (позиция, место)

это структурный элемент представления чисел в позиционных системах счисления. Разряд является «рабочим местом» цифры в числе. Порядковому номеру разряда соответствует его вес — множитель, на который надо умножить значение разряда в данной системе счисления. Диапазон значений для всех разрядов (в данной системе счисления) неизменен.

В десятичной системе счисления число 421 равняется
    421 = 4 * 10^2 + 2 * 10^1 + 1 * 10^0,
то есть, цифра в нулевом разряде (справа, начиная с нуля) умножается на 10 в нулевой степени. Цифра в первом разряде — на 10 в первой степени, и т. д."

Позиционная система счисления обладает рядом свойств:

Основание системы счисления в ней самой всегда записывается как 10; например, в двоичной системе счисления 10 означает число 2.
"Естественный порядок на натуральных числах соответствует лексикографическому порядку на их представлениях в позиционной системе счисления. Поэтому сравнивать их представления можно поразрядно, начиная со старшего разряда, до тех пор, пока цифра в одном числе не будет больше соответствующей цифры в другом. Например, для сравнения чисел 321 и 312 в десятичной системе счисления нужно сравнивать цифры в одинаковых разрядах слева направо:
3 = 3 — результат сравнения чисел пока не определён;
2 > 1 — первое число больше (независимо от оставшихся цифр)."
Арифметические операции над числами. Позиционная система счисления позволяет без труда выполнять сложение, вычитание, умножение, деление и деление с остатком чисел, зная только таблицу сложения однозначных чисел, а для трёх последних операций ещё и таблицу умножения в соответствующей системе.

---

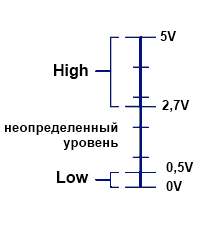
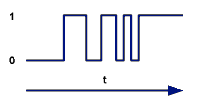
Люди предпочитают десятичную систему счисления вероятно потому, что с древних времен они считали по пальцам, а пальцев у людей по 10 на руках и ногах. Для цифровой электроники очень удобна двоичная система счисления (есть сигнал 1, нет сигнала 0). В связи с этим описание внутренних процессов и представление данных в ЭВМ используют именно ее. Для общения с ЭВМ используют, кроме двоичной, десятичную, восьмеричную и шестнадцатеричную системы счисления. Понимание принципов построения позиционных систем счисления необходимо на всех этапах проектирования и обслуживания цифровых систем.

---

Десятичная система счисления

позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами.
Один десятичный разряд в десятичной системе счисления иногда называют декадой. В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.
Например, число сто три представляется в десятичной системе счисления в виде:
    103 = 1 * 10^{2} + 0 * 10^{1} + 3* 10^{0}.

---

Двоичная система счисления

позиционная система счисления с основанием 2. В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 5₁₀, в двоичной 101₂.

операции с двоичными данными

Таблица сложения
+	0	1
0	0	1
1	1	10(перенос в старший разряд)

Таблица вычитания
-	0	1
0	0	1
1	(заём из старшего разряда) 1	1

Таблица умножения
x	0	1
0	0	0
1	0	1

---

Шестнадцатеричная систем счисления

позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.
Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде.
hexadecimal - Отсюда происходит использование в конце шестнадцатеричных чисел латинской буквы Н наряду с индексом 16 для обозначения шестнадцатеричной системы счисления. Мы будем использовать также термин Н-код.

операции с шестнадцатеричными данными

Каждый шестнадцатеричный символ может быть представлен единственным сочетанием четырех бит. Таким образом, представлением двоичного числа 1001 1110 в шестнадцатеричном коде является число 9Е. Эго значит, что часть 1001 двоичного числа равна 9, а часть 1110 равна Е (конечно, в шестнадцатеричном коде). Следовательно, 1001 1110₂=9E₁₆. (Не следует забывать, что индексы означают основание системы счисления.)
Как преобразовать двоичное число 111010 в шестнадца¬теричное? Надо начать с МБ и разделить двоичное число на группы из 4 бит. Затем надо заменить каждую группу из 4 бит эквивалентной шестнадцатеричной цифрой: 1010₂ = А, 0011₂ = 3, следовательно, 111010₂=ЗА₁₆.
Как преобразовать шестнадцатеричное число 7F в двоичное? В этом случае каждая шестнадцатеричная цифра должна быть заменена своим двоичным эквивалентом из 4 бит. В примере двоичное число 0111 заменено шестнадцатеричной цифрой 7, а 1111₂ заменяет F,6, откуда 7F₁₆ = = 1111 0111₂.

---

соответствие записей чисел в различных системах счисления

запись	соответствие записей чисел в различных системах счисления
десятичная	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
двоичная	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111	0001 0000
шестнадцатиричная	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10

---